On property (T) for $\operatorname{Aut}(F_n)$ and $\operatorname{SL}_n(\mathbb{Z})$
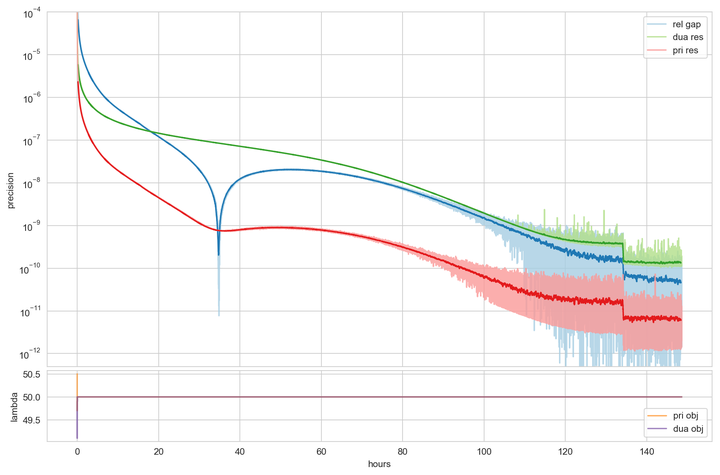 SCS progress on Adj₅ + 3Op₅ - 50Δ₅
SCS progress on Adj₅ + 3Op₅ - 50Δ₅
Abstract
We prove that $\operatorname{Aut}(F_n)$ has Kazhdan’s property (T) for every $n \geqslant 6$. Our proof relies on relating the Laplace operators of $\operatorname{SAut}(F_n)$ for various $n$ via symmetrisation by torsion. The key step involves a computation in the group ring of $\operatorname{SAut}(F_5)$. The method works also for $\operatorname{SL}_n(\mathbb{Z})$ and for $n \geqslant 3$ yields a new proof of the fact that $\operatorname{SL}_n(\mathbb{Z})$ has property (T).
Additionally, in both families of groups we show that it is enough to study the ball of radius $4$ in the usual Cayley graphs to conclude that the groups have property (T).
We also provide explicit lower bounds for the Kazhdan constants of $\operatorname{SAut}(F_n)$ (with $n \geqslant 6$) and of $\operatorname{SL}_n(\mathbb{Z})$ (with $n \geqslant 3$) with respect to natural generating sets.In the latter case, these bounds improve upon previously known lower bounds whenever $n\geqslant 6$.
Replication details for computations with special linear groups as described in Section 5.1 of the paper are reproduced in a separate document.
For exact details of computations e.g. for $\operatorname{Adj}_5 + 3 \operatorname{Op}_5) - 1.4\Delta_5 \in I\operatorname{SAut}(F_5)$ see the document deposited with the dataset in zenodo data repository.