using Pkg
Pkg.activate(@__DIR__)
Pkg.status()
Interactive polyhedral computation with Jupyter+Julia+
¶
by Marek Kaluba (TU Berlin, AMU Poznań), Sascha Timme (TU Berlin), Benjamin Lorenz (TU Berlin)
Polymake.jl¶
A new interface to polymake using Julia
Developed as part of the OSCAR project
Open development at github.com/oscar-system/Polymake.jl
Installation¶
import Pkg
Pkg.add("Polymake")
Pkg.status()
using Polymake
Functionality¶
The polymake objects a user encounters can roughly be divided in three classes
- big objects (e.g., cones, polytopes, simplicial complexes),
- small objects (e.g., matrices, polynomials, tropical numbers),
- user functions
All* are easily accessible through Polymake.jl.
Big objects¶
Broadly speaking, big objects correspond to mathematical concepts with well defined semantics.
p = polytope.Polytope(POINTS=[1 1 2; 1 3 4])
Big objects can be e queried for their properties (they are only computed when queried for the first time)
p.VERTICES
p
The documentation is also accessible from the package (though still in perl syntax):
?polytope.rand_sphere
p = @pm polytope.rand_sphere{AccurateFloat}(3, 10)
Small objects¶
Small objects correspond to types or data structures which are implemented in C++.
p.VERTICES
dump(p.VERTICES)
Small objects follow the Julia semantics and expected behaviour as closely as possible
# Indexing works
p.VERTICES[1, :]
# Conversion to native Julia types
Matrix{Rational{BigInt}}(p.VERTICES)
float.([sum(x->x^2, r) - 1 for r in eachrow(p.VERTICES)])
Caveat: Some small types are not yet wrapped¶
K₅ = graph.complete(5)
K₅.MAX_CLIQUES
Sometimes you can use the @convert_to macro to convert to a wrapped type.
max_cliques = @convert_to Array{Set} K₅.MAX_CLIQUES
Set(max_cliques[1])
Example¶
An advantage of the package is that it allows effortless combination of computations in polyhedral geometry with e.g., state-of-the-art numerical software. In particular, we combine
We test a theoretical result from Soprunova and Sottile on non-trivial lower bounds for the number of real solutions to sparse polynomial systems.
Evgenia Soprunova and Frank Sottile. "Lower bounds for real solutions to sparse polynomial systems." Advances in Mathematics 204.1 (2006): 116-151.
We start with the 10 lattice points $A=\{a_1,\ldots,a_{10}\} \subset \mathbb{Z}^2$ of the scaled two-dimensional simplex $3\Delta_2$ and look at the regular triangulation $\mathcal{T}$ induced by the lifting $\lambda = [12, 3, 0, 0, 8, 1, 0, 9, 5, 15]$.
A = polytope.lattice_points(polytope.simplex(2,3));
λ = [12, 3, 0, 0, 8, 1, 0, 9, 5, 15];
F = polytope.regular_subdivision(A, λ);
T = topaz.GeometricSimplicialComplex(COORDINATES = A[:,2:end], FACETS = F)
The triangulation $\mathcal{T}$ is very special in that it is foldable (or "balanced"), i.e., the dual graph is bipartite.
This means that the triangles can be colored, say, black and white such that no two triangles of the same color share an edge.
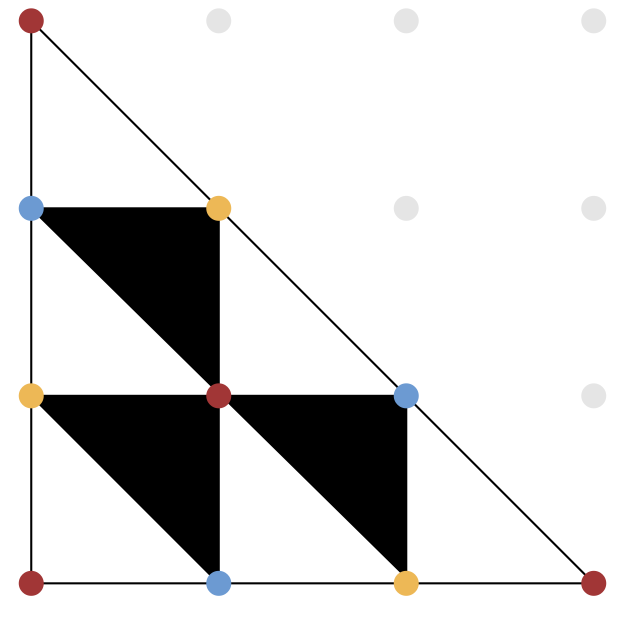The signature $\sigma(\mathcal{T})$ of a balanced triangulation of a polygon is the absolute value of the difference of the number of white triangles and the number of the black triangles whose normalized volume is odd.
(foldable = T.FOLDABLE, signature = T.SIGNATURE)
Now, a Wroński polynomial $W_{\mathcal{T},s}(x)$ has the lifted lattice points as exponents, and only one non-zero coefficient $c_i \in \mathbb{R}$ per color class of vertices of the triangulation $$W_{\mathcal{T},s}(x) = \sum_{i=0}^d c_i \left (\sum_{j:\;\textrm{color($a_j$)=$i$}} s^{\lambda_i} x^{a_j} \right ) \,.$$
A Wroński system consists of $d$ Wroński polynomials with respect to the same lattice points $A$ and lifting $\lambda$ such that for general $s = s_0 \in [0,1]$ it has precisely $d!\operatorname{vol}(\operatorname{conv}(A))$ distinct complex solutions, which is the highest possible number by Kushnirenko’s Theorem.
Soprunova and Sottile showed that a Wroński system has at least $\sigma(\mathcal{T})$ distinct real solutions if two conditions are satisfied.
1) A certain double cover of the real toric variety associated with $A$ must be orientable (this is the case here)
2) The Wroński center ideal, a zero-dimensional ideal in coordinates $x_1,x_2$ and $s$ depending on $\mathcal{T}$, has no real roots with $s$ coordinate between 0 and 1.
Goal: Verify condition 2) using HomotopyContinuation.jl.
Luckily, polymake already has an implementationof the Wroński center ideal
I = polytope.wronski_center_ideal(A, λ)
collect(I.GENERATORS)
We have to convert the ideal returned by Polymake.jl to a polynomial system which HomotopyContinuation.jl understands.
using HomotopyContinuation
# define a small helper function
function hc_poly(f, vars)
M = Polymake.monomials_as_matrix(f)
monomials = [prod(vars.^m) for m in eachrow(M)]
coeffs = convert.(Int, Polymake.coefficients_as_vector(f))
sum(map(*, coeffs, monomials))
end
@polyvar x[1:2] s;
HC_I = [hc_poly(f, [x;s]) for f in I.GENERATORS]
Since we are only interested in solutions in the algebraic torus $(\mathbb{C}^*)^3$ we can use a polyhedral homotopy to efficiently compute the solutions.
@time res = HomotopyContinuation.solve(HC_I; start_system = :polyhedral, only_torus = true)
Out of the 54 complex roots only two solutions are real. Strictly speaking, this is here only checked heuristically by looking at the size of the imaginary parts.
HomotopyContinuation.real_solutions(res)
We see that no solution has the $s$-coordinate in $(0,1)$.
By Soprunova and Sottile result, the Wroński system with respect to $A$ and $\lambda$ for $s=1$ has at least $\sigma(\mathcal{T})=3$ real solutions. Let us verify this on an example.
c = Vector{Rational}[[19,8,-19], [39,7,42]]
W = polytope.wronski_system(A, λ, c, 1)
HC_W = [hc_poly(f, x) for f in W.GENERATORS]
W_res = HomotopyContinuation.solve(HC_W)
Finally, we can use the ImplicitPlots.jl package to visualize the real solutions of the Wroński system W.
W_real = HomotopyContinuation.real_solutions(W_res)
using ImplicitPlots, Plots;
plt = plot(aspect_ratio = :equal);
implicit_plot!(plt, HC_W[1]);
implicit_plot!(plt, HC_W[2]; color=:indianred);
scatter!(first.(W_real), last.(W_real), markercolor=:black)